bruges.filters package#

Submodules#

bruges.filters.anisodiff module#

bruges.filters.anisodiff.anisodiff(img, niter=1, kappa=50, gamma=0.1, step=(1.0, 1.0), option=1)[source]#

Anisotropic diffusion.

Usage: imgout = anisodiff(im, niter, kappa, gamma, option)

Parameters

image (img - input) –
iterations (niter - number of) –
? (kappa - conduction coefficient 20-100) –
stability (gamma - max value of .25 for) –
tuple (step -) –
in (the distance between adjacent pixels) –
1 (option - 1 Perona Malik diffusion equation No) – 2 Perona Malik diffusion equation No 2

Returns

imgout - diffused image.

kappa controls conduction as a function of gradient. If kappa is low small intensity gradients are able to block conduction and hence diffusion across step edges. A large value reduces the influence of intensity gradients on conduction.

gamma controls speed of diffusion (you usually want it at a maximum of 0.25)

step is used to scale the gradients in case the spacing between adjacent pixels differs in the x and y axes

Diffusion equation 1 favours high contrast edges over low contrast ones. Diffusion equation 2 favours wide regions over smaller ones.

bruges.filters.anisodiff.anisodiff3(stack, niter=1, kappa=50, gamma=0.1, step=(1.0, 1.0, 1.0), option=1)[source]#

3D Anisotropic diffusion.

Usage: stackout = anisodiff(stack, niter, kappa, gamma, option)

Parameters

stack (stack - input) –
iterations (niter - number of) –
? (kappa - conduction coefficient 20-100) –
stability (gamma - max value of .25 for) –
tuple (step -) –
in (the distance between adjacent pixels) –
1 (option - 1 Perona Malik diffusion equation No) – 2 Perona Malik diffusion equation No 2

Returns

stackout - diffused stack.

gamma controls speed of diffusion (you usually want it at a maximum of 0.25)

step is used to scale the gradients in case the spacing between adjacent pixels differs in the x,y and/or z axes

Diffusion equation 1 favours high contrast edges over low contrast ones. Diffusion equation 2 favours wide regions over smaller ones.

bruges.filters.convolve module#

bruges.filters.convolve.convolve(arr, v, axis=- 1, verbose=False)[source]#

Convolve n-dimensional arr with a 1D wavelet or 2D wavelet bank.

Parameters

arr (ndarray) – The trace, or 2D section, or volume.
v (ndarray) – The wavelet, must be 1D function or a 2D wavelet ‘bank’. If a wavelet bank, time should be on the last axis.
axis (int) – The time axis of the arr data. In other words, the axis corresponding to a single ‘trace’. If you index into this axis, you will get a single ‘trace’.
verbose (bool) – If True, print out the shapes of the inputs and output.

Returns

Discrete, linear convolution of arr and v.

Return type

ndarray

bruges.filters.filters module#

bruges.filters.filters.conservative(arr, size=5, supercon=False)[source]#

Conservative, a nonlinear n-D despiking filter. Very conservative! Only changes centre value if it is outside the range of all the other values in the kernel. Read http://subsurfwiki.org/wiki/Conservative_filter

Parameters

arr (ndarray) – an n-dimensional array, such as a seismic horizon.
size (int) – the kernel size, e.g. 5 for 5x5 (in a 2D arr). Should be odd, rounded up if not.
supercon (bool) – whether to be superconservative. If True, replaces pixel with min or max of kernel. If False (default), replaces pixel with mean of kernel.

Returns

the resulting smoothed array.

Return type

ndarray

bruges.filters.filters.kuwahara(arr, size=5)[source]#

Kuwahara, a nonlinear 2D smoothing filter. http://subsurfwiki.org/wiki/Kuwahara_filter

Parameters

arr (ndarray) – a 2D array, such as a seismic horizon.
size (int) – the kernel size, e.g. 5 for 5x5. Should be odd, rounded up if not.

Returns

the resulting smoothed array.

Return type

ndarray

bruges.filters.filters.mean(arr, size=5)[source]#

A linear n-D smoothing filter. Can be used as a moving average on 1D data.

Parameters

arr (ndarray) – an n-dimensional array, such as a seismic horizon.
size (int) – the kernel size, e.g. 5 for 5x5. Should be odd, rounded up if not.

Returns

the resulting smoothed array.

Return type

ndarray

bruges.filters.filters.median(arr, size=5)[source]#

A nonlinear n-D edge-preserving smoothing filter.

Parameters

arr (ndarray) – an n-dimensional array, such as a seismic horizon.
size (int) – the kernel size, e.g. 5 for 5x5. Should be odd, rounded up if not.

Returns

the resulting smoothed array.

Return type

ndarray

bruges.filters.filters.mode(arr, size=5, tie='smallest')[source]#

A nonlinear n-D categorical smoothing filter. Use this to filter non- continuous variables, such as categorical integers, e.g. to label facies.

Parameters

arr (ndarray) – an n-dimensional array, such as a seismic horizon.
size (int) – the kernel size, e.g. 5 for 5x5. Should be odd, rounded up if not.
tie (str) – ‘smallest’ or ‘largest’. In the event of a tie (i.e. two or more values having the same count in the kernel), whether to give back the smallest of the tying values, or the largest.

Returns

the resulting smoothed array.

Return type

ndarray

bruges.filters.filters.rms(arr, size=5)[source]#

A linear n-D smoothing filter. Can be used as a moving average on 1D data.

Parameters

arr (ndarray) – an n-dimensional array, such as a seismic horizon.
size (int) – the kernel size, e.g. 5 for 5x5. Should be odd, rounded up if not.

Returns

the resulting smoothed array.

Return type

ndarray

bruges.filters.filters.rotate_phase(s, phi, degrees=False)[source]#

Performs a phase rotation of wavelet or wavelet bank using:

\[A = w(t)\cos\phi - h(t)\sin\phi\]

where w(t) is the wavelet, h(t) is its Hilbert transform, and phi is the phase rotation angle (default is radians).

The analytic signal can be written in the form \(S(t) = A(t)e^{j\theta (t)}\) where \(A(t) = \left| h(w(t)) \right|\) and \(\theta(t) = \tan^{-1}[h(w(t))]\). A(t) is called the “reflection strength” and \(\phi(t)\) is called the “instantaneous phase”.

A constant phase rotation \(\phi\) would produce the analytic signal \(S(t)=A(t)e^{j(\theta(t) + \phi)}\). To get the non-analytic signal, we take

\[\begin{split}real(S(t)) &= A(t)\cos(\theta(t) + \phi) \\ &= A(t)\cos\theta(t)\cos(\phi)-\sin\theta(t)\sin(\phi))\\ &= w(t)\cos\phi-h(t)\sin\phi\end{split}\]

Parameters

w (ndarray) – The wavelet vector, can be a 2D wavelet bank.
phi (float) – The phase rotation angle (in radians) to apply.
degrees (bool) – If phi is in degrees not radians.

Returns

The phase rotated signal (or bank of signals).

bruges.filters.filters.snn(arr, size=5, include=True)[source]#

Symmetric nearest neighbour, a nonlinear 2D smoothing filter. http://subsurfwiki.org/wiki/Symmetric_nearest_neighbour_filter

Parameters

arr (ndarray) – a 2D array, such as a seismic horizon.
size (int) – the kernel size, e.g. 5 for 5x5. Should be odd, rounded up if not.
include (bool) – whether to include the central pixel itself.

Returns

the resulting smoothed array.

Return type

ndarray

bruges.filters.kernels module#

bruges.filters.kernels.gaussian(size, size_y=None)[source]#

2D Gaussian Kernel

Parameters

size (int) – the kernel size, e.g. 5 for 5x5 (in a 2D arr). Should be odd, rounded up if not.
size_y (int) – similar to size. If not provided, uses size as default.

Returns: a Gaussian kernel.

bruges.filters.kernels.gaussian_kernel(size, size_y=None)#

2D Gaussian Kernel

Parameters

size (int) – the kernel size, e.g. 5 for 5x5 (in a 2D arr). Should be odd, rounded up if not.
size_y (int) – similar to size. If not provided, uses size as default.

Returns: a Gaussian kernel.

bruges.filters.wavelets module#

bruges.filters.wavelets.berlage(duration, dt, f, n=2, alpha=180, phi=- 1.5707963267948966, t=None, return_t=True, sym=True)[source]#

Generates a Berlage wavelet with a peak frequency f. Implements

\[w(t) = AH(t) t^n \mathrm{e}^{- \alpha t} \cos(2 \pi f_0 t + \phi_0)\]

as described in Aldridge, DF (1990), The Berlage wavelet, GEOPHYSICS 55 (11), p 1508-1511. Berlage wavelets are causal, minimum phase and useful for modeling marine airgun sources.

If you pass a 1D array of frequencies, you get a wavelet bank in return.

(Source code, png, hires.png, pdf)

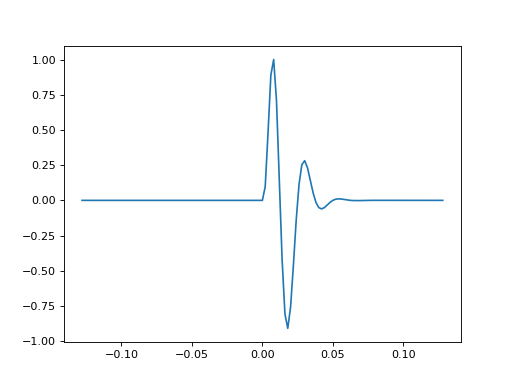
Parameters

duration (float) – The length in seconds of the wavelet.
dt (float) – The sample interval in seconds (often one of 0.001, 0.002, or 0.004).
f (array-like) – Centre frequency of the wavelet in Hz. If a sequence is passed, you will get a 2D array in return, one row per frequency.
n (float) – The time exponent; non-negative and real.
alpha (float) – The exponential decay factor; non-negative and real.
phi (float) – The phase.
t (array-like) – The time series to evaluate at, if you don’t want one to be computed. If you pass t then duration and dt will be ignored, so we recommend passing None for those arguments.
return_t (bool) – If True, then the function returns a tuple of wavelet, time-basis.
sym (bool) – If True (default behaviour before v0.5) then the wavelet is forced to have an odd number of samples and the central sample is at 0 time.

Returns

ndarray. Berlage wavelet(s) with centre frequency f sampled on t. If: you passed return_t=True then a tuple of (wavelet, t) is returned.

bruges.filters.wavelets.cosine(duration, dt, f, t=None, return_t=True, taper='gaussian', sigma=None, sym=True)[source]#

With the default Gaussian window, equivalent to a ‘modified Morlet’ also sometimes called a ‘Gabor’ wavelet. The bruges.filters.gabor function returns a similar shape, but with a higher mean frequancy, somewhere between a Ricker and a cosine (pure tone).

If you pass a 1D array of frequencies, you get a wavelet bank in return.

(Source code, png, hires.png, pdf)

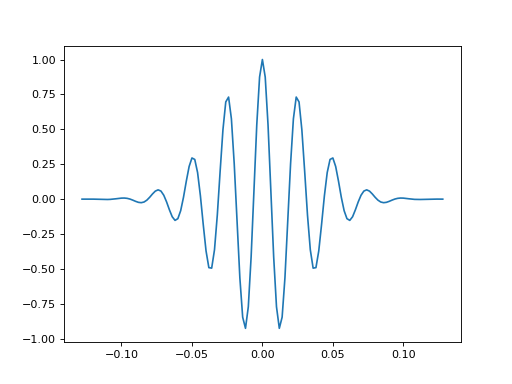
Parameters

duration (float) – The length in seconds of the wavelet.
dt (float) – The sample interval in seconds (often one of 0.001, 0.002, or 0.004).
f (array-like) – Dominant frequency of the wavelet in Hz. If a sequence is passed, you will get a 2D array in return, one row per frequency.
t (array-like) – The time series to evaluate at, if you don’t want one to be computed. If you pass t then duration and dt will be ignored, so we recommend passing None for those arguments.
return_t (bool) – If True, then the function returns a tuple of wavelet, time-basis.
taper (str or function) – The window or tapering function to apply. To use one of NumPy’s functions, pass ‘bartlett’, ‘blackman’ (the default), ‘hamming’, or ‘hanning’; to apply no tapering, pass ‘none’. To apply your own function, pass a function taking only the length of the window and returning the window function.
sigma (float) – Width of the default Gaussian window, in seconds. Defaults to 1/8 of the duration.

Returns

ndarray. sinc wavelet(s) with centre frequency f sampled on t. If: you passed return_t=True then a tuple of (wavelet, t) is returned.

bruges.filters.wavelets.gabor(duration, dt, f, t=None, return_t=True, sym=True)[source]#

Generates a Gabor wavelet with a peak frequency f0 at time t.

https://en.wikipedia.org/wiki/Gabor_wavelet

If you pass a 1D array of frequencies, you get a wavelet bank in return.

(Source code, png, hires.png, pdf)

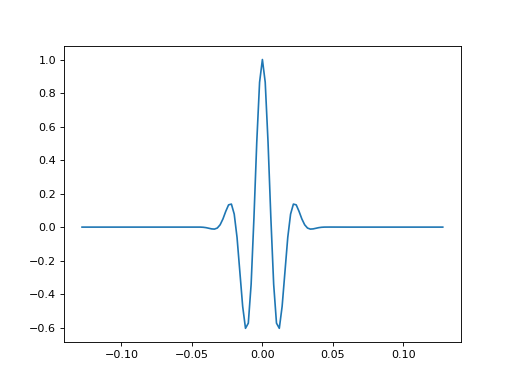
Parameters

duration (float) – The length in seconds of the wavelet.
dt (float) – The sample interval in seconds (often one of 0.001, 0.002, or 0.004).
f (array-like) – Centre frequency of the wavelet in Hz. If a sequence is passed, you will get a 2D array in return, one row per frequency.
t (array-like) – The time series to evaluate at, if you don’t want one to be computed. If you pass t then duration and dt will be ignored, so we recommend passing None for those arguments.
return_t (bool) – If True, then the function returns a tuple of wavelet, time-basis.

Returns

ndarray. Gabor wavelet(s) with centre frequency f sampled on t. If: you passed return_t=True then a tuple of (wavelet, t) is returned.

bruges.filters.wavelets.generalized(duration, dt, f, u=2, t=None, return_t=True, imag=False, sym=True)[source]#

Wang’s generalized wavelet, of which the Ricker is a special case where u = 2. The parameter u is the order of the time-domain derivative, which can be a fractional derivative.

As given by Wang (2015), Generalized seismic wavelets. GJI 203, p 1172-78. DOI: https://doi.org/10.1093/gji/ggv346. I am using the (more accurate) frequency domain method (eq 4 in that paper).

(Source code, png, hires.png, pdf)

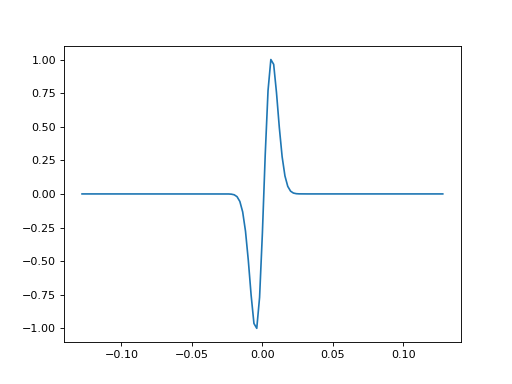
Parameters

duration (float) – The length of the wavelet, in s.
dt (float) – The time sample interval in s.
f (float or array-like) – The frequency or frequencies, in Hertz.
u (float or array-like) – The fractional derivative parameter u.
t (array-like) – The time series to evaluate at, if you don’t want one to be computed. If you pass t then duration and dt will be ignored, so we recommend passing None for those arguments.
return_t (bool) – Whether to return the time basis array.
center (bool) – Whether to center the wavelet on time 0.
imag (bool) – Whether to return the imaginary component as well.
sym (bool) – If True (default behaviour before v0.5) then the wavelet is forced to have an odd number of samples and the central sample is at 0 time.

Returns

ndarray. If f and u are floats, the resulting wavelet has duration/dt: = A samples. If you give f as an array of length M and u as an array of length N, then the resulting wavelet bank will have shape (M, N, A). If f or u are floats, their size will be 1, and they will be squeezed out: the bank is always squeezed to its minimum number of dimensions. If you passed return_t=True then a tuple of (wavelet, t) is returned.

bruges.filters.wavelets.klauder(duration, dt, f, autocorrelate=True, t=None, return_t=True, taper='blackman', sym=True, **kwargs)[source]#

By default, gives the autocorrelation of a linear frequency modulated wavelet (sweep). Uses scipy.signal.chirp, adding dimensions as necessary.

(Source code, png, hires.png, pdf)

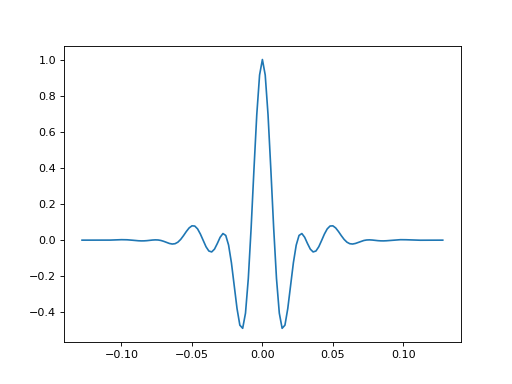
Parameters

duration (float) – The length in seconds of the wavelet.
dt (float) – is the sample interval in seconds (usually 0.001, 0.002, or 0.004)
f (array-like) – Upper and lower frequencies. Any sequence like (f1, f2). A list of lists will create a wavelet bank.
autocorrelate (bool) – Whether to autocorrelate the sweep(s) to create a wavelet. Default is True.
t (array-like) – The time series to evaluate at, if you don’t want one to be computed. If you pass t then duration and dt will be ignored, so we recommend passing None for those arguments.
return_t (bool) – If True, then the function returns a tuple of wavelet, time-basis.
taper (str or function) – The window or tapering function to apply. To use one of NumPy’s functions, pass ‘bartlett’, ‘blackman’ (the default), ‘hamming’, or ‘hanning’; to apply no tapering, pass ‘none’. To apply your own function, pass a function taking only the length of the window and returning the window function.
sym (bool) – If True (default behaviour before v0.5) then the wavelet is forced to have an odd number of samples and the central sample is at 0 time.
**kwargs – Further arguments are passed to scipy.signal.chirp. They are method (‘linear’,’quadratic’,’logarithmic’), phi (phase offset in degrees), and vertex_zero.

Returns

The waveform. If you passed return_t=True then a tuple of: (wavelet, t) is returned.

Return type

ndarray

bruges.filters.wavelets.ormsby(duration, dt, f, t=None, return_t=True, sym=True)[source]#

The Ormsby wavelet requires four frequencies which together define a trapezoid shape in the spectrum. The Ormsby wavelet has several sidelobes, unlike Ricker wavelets.

(Source code, png, hires.png, pdf)

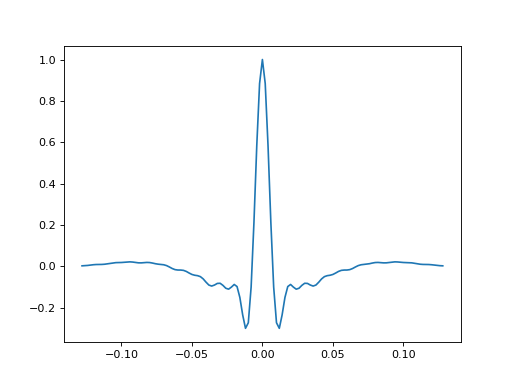
Parameters

duration (float) – The length in seconds of the wavelet.
dt (float) – The sample interval in seconds (usually 0.001, 0.002, or 0.004).
f (array-like) – Sequence of form (f1, f2, f3, f4), or list of lists of frequencies, which will return a 2D wavelet bank.
t (array-like) – The time series to evaluate at, if you don’t want one to be computed. If you pass t then duration and dt will be ignored, so we recommend passing None for those arguments.
return_t (bool) – If True, then the function returns a tuple of wavelet, time-basis.
sym (bool) – If True (default behaviour before v0.5) then the wavelet is forced to have an odd number of samples and the central sample is at 0 time.

Returns

A vector containing the Ormsby wavelet, or a bank of them. If: you passed return_t=True then a tuple of (wavelet, t) is returned.

Return type

ndarray

bruges.filters.wavelets.ormsby_fft(duration, dt, f, P=(0, 0), return_t=True, sym=True)[source]#

Non-white Ormsby, with arbitary amplitudes.

Can use as many points as you like. The power of f1 and f4 is assumed to be 0, so you only need to provide p2 and p3 (the corners). (You can actually provide as many f points as you like, as long as there are n - 2 matching p points.)

(Source code, png, hires.png, pdf)

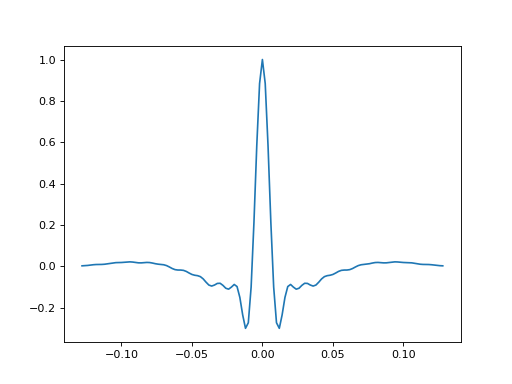
Parameters

duration (float) – The length in seconds of the wavelet.
dt (float) – The sample interval in seconds (usually 0.001, 0.002, or 0.004).
f (array-like) – Sequence of form (f1, f2, f3, f4), or list of lists of frequencies, which will return a 2D wavelet bank.
P (tuple) – The power of the f2 and f3 frequencies, in relative dB. (The magnitudes of f1 and f4 are assumed to be -∞ dB, i.e. a magnitude of 0.) The default power values of (0, 0) results in a trapezoidal spectrum and a conventional Ormsby wavelet. Pass, e.g. (0, -15) for a ‘pink’ wavelet, with more energy in the lower frequencies.
return_t (bool) – If True, then the function returns a tuple of wavelet, time-basis.
sym (bool) – If True (default behaviour before v0.5) then the wavelet is forced to have an odd number of samples and the central sample is at 0 time.

Returns

A vector containing the Ormsby wavelet, or a bank of them. If: you passed return_t=True then a tuple of (wavelet, t) is returned.

Return type

ndarray

bruges.filters.wavelets.ricker(duration, dt, f, t=None, return_t=True, sym=True)[source]#

Also known as the mexican hat wavelet, models the function:

\[A = (1 - 2 \pi^2 f^2 t^2) e^{-\pi^2 f^2 t^2}\]

If you pass a 1D array of frequencies, you get a wavelet bank in return.

(Source code, png, hires.png, pdf)

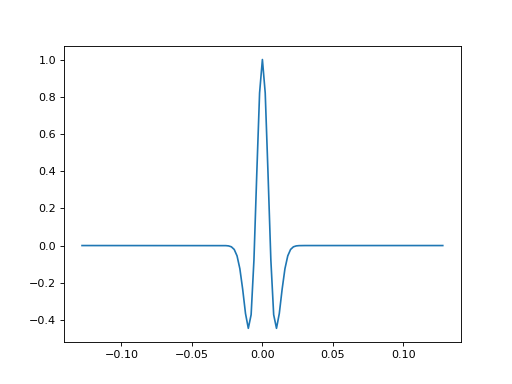
Parameters

duration (float) – The length in seconds of the wavelet.
dt (float) – The sample interval in seconds (often one of 0.001, 0.002, or 0.004).
f (array-like) – Centre frequency of the wavelet in Hz. If a sequence is passed, you will get a 2D array in return, one row per frequency.
t (array-like) – The time series to evaluate at, if you don’t want one to be computed. If you pass t then duration and dt will be ignored, so we recommend passing None for those arguments.
return_t (bool) – If True, then the function returns a tuple of wavelet, time-basis.
sym (bool) – If True (default behaviour before v0.5) then the wavelet is forced to have an odd number of samples and the central sample is at 0 time.

Returns

ndarray. Ricker wavelet(s) with centre frequency f sampled on t. If: you passed return_t=True then a tuple of (wavelet, t) is returned.

bruges.filters.wavelets.sinc(duration, dt, f, t=None, return_t=True, taper='blackman', sym=True)[source]#

sinc function centered on t=0, with a dominant frequency of f Hz.

If you pass a 1D array of frequencies, you get a wavelet bank in return.

(Source code, png, hires.png, pdf)

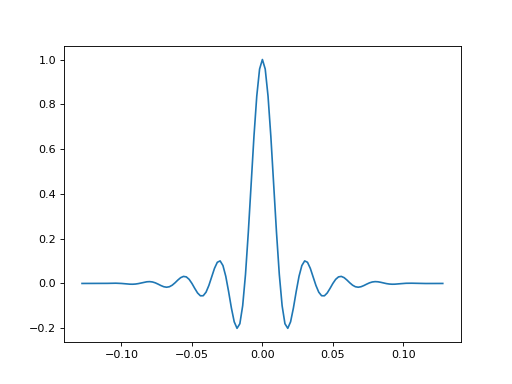
Parameters

duration (float) – The length in seconds of the wavelet.
dt (float) – The sample interval in seconds (often one of 0.001, 0.002, or 0.004).
f (array-like) – Dominant frequency of the wavelet in Hz. If a sequence is passed, you will get a 2D array in return, one row per frequency.
t (array-like) – The time series to evaluate at, if you don’t want one to be computed. If you pass t then duration and dt will be ignored, so we recommend passing None for those arguments.
return_t (bool) – If True, then the function returns a tuple of wavelet, time-basis.
taper (str or function) – The window or tapering function to apply. To use one of NumPy’s functions, pass ‘bartlett’, ‘blackman’ (the default), ‘hamming’, or ‘hanning’; to apply no tapering, pass ‘none’. To apply your own function, pass a function taking only the length of the window and returning the window function.

Returns

ndarray. sinc wavelet(s) with centre frequency f sampled on t. If: you passed return_t = True then a tuple of (wavelet, t) is returned.

bruges.filters.wavelets.sweep(duration, dt, f, autocorrelate=True, t=None, return_t=True, taper='blackman', sym=True, **kwargs)#

By default, gives the autocorrelation of a linear frequency modulated wavelet (sweep). Uses scipy.signal.chirp, adding dimensions as necessary.

(Source code, png, hires.png, pdf)

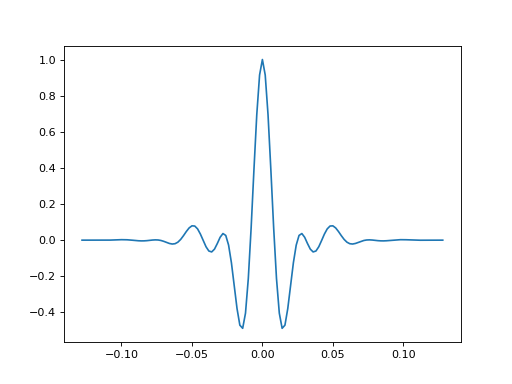
Parameters

duration (float) – The length in seconds of the wavelet.
dt (float) – is the sample interval in seconds (usually 0.001, 0.002, or 0.004)
f (array-like) – Upper and lower frequencies. Any sequence like (f1, f2). A list of lists will create a wavelet bank.
autocorrelate (bool) – Whether to autocorrelate the sweep(s) to create a wavelet. Default is True.
t (array-like) – The time series to evaluate at, if you don’t want one to be computed. If you pass t then duration and dt will be ignored, so we recommend passing None for those arguments.
return_t (bool) – If True, then the function returns a tuple of wavelet, time-basis.
taper (str or function) – The window or tapering function to apply. To use one of NumPy’s functions, pass ‘bartlett’, ‘blackman’ (the default), ‘hamming’, or ‘hanning’; to apply no tapering, pass ‘none’. To apply your own function, pass a function taking only the length of the window and returning the window function.
sym (bool) – If True (default behaviour before v0.5) then the wavelet is forced to have an odd number of samples and the central sample is at 0 time.
**kwargs – Further arguments are passed to scipy.signal.chirp. They are method (‘linear’,’quadratic’,’logarithmic’), phi (phase offset in degrees), and vertex_zero.

Returns

The waveform. If you passed return_t=True then a tuple of: (wavelet, t) is returned.

Return type

ndarray

bruges.filters package#

Submodules#

bruges.filters.anisodiff module#

bruges.filters.convolve module#

bruges.filters.filters module#

bruges.filters.kernels module#

bruges.filters.wavelets module#

Module contents#